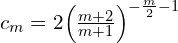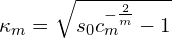Users of Leapfrog Geo will probably recognise the term ‘spheroidal‘ from the geometric and numerical modelling tools available in Leapfrog Geo. The choice (and parameters) of this interpolant function (linear or spheroidal) changes the behaviour of modelled geological or grade iso-surfaces.
The spheroidal family of variogram models were developed by Seequent. While the spheroidal has since been incorporated into Snowden’s Supervisor, it is not generally available in other resource estimation packages.
With the development of Leapfrog Edge, spheroidal variogram models are now available within our dynamic resource estimation solution (alongside industry standard spatial models), where they can be utilised in kriged grade estimation.
Resource estimation practitioners need to understand and trust the algorithms underlying their models, and a number of customers have asked us for details of the mathematics underlying the spheroidal variogram model.
In this blog, Mike Stewart, a Technical Domain Expert at Seequent, explains the maths behind the Spheroidal family of variograms in Leapfrog Edge.
Hold onto your hats.
The spheroidal variogram model was developed by Seequent, primarily for use in RBF interpolants. Seequent wanted an effectively compact spatial function that has linear behaviour near the origin and an asymptotic approach to the sill. This was developed by taking a commonly used family of radial functions and linearizing them near the origin.
That family is the inverse multi-quadric functions, which are also referred to as the generalised Cauchy family in the geostatistics community. In this document we will use the term multiquadric. They have a shape similar to the more familiar Gaussian model – smooth at the origin, rising rapidly at first, then asymptotically approaching the sill. The shape of the curve therefore has an inflexion point, and it is at this point it makes sense for the linearization to occur.
We will start by defining the family of generalised multiquadric models. Next, we will consider the characteristics of the resultant spheroidal model and the modifications that need to be made. Finally, the specifics of the transformation will be detailed.
1. Characteristics
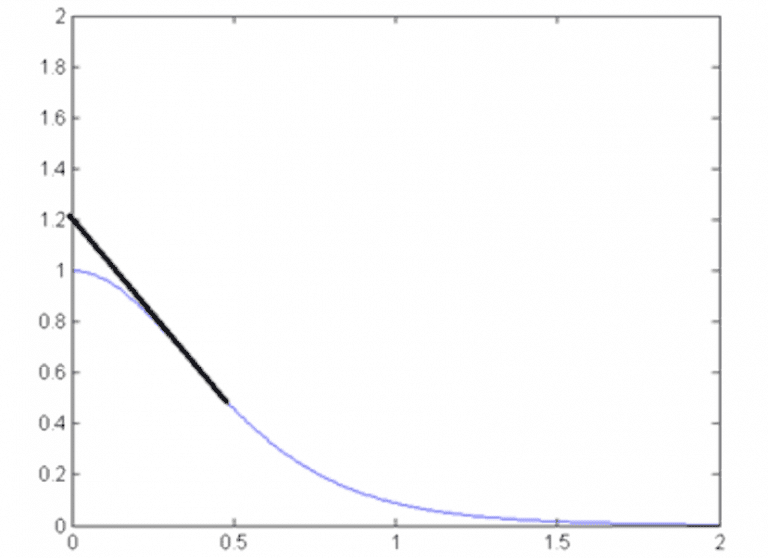
The shape and characteristics of the final standardised spheroidal variogram model can be seen below in Figure 1.
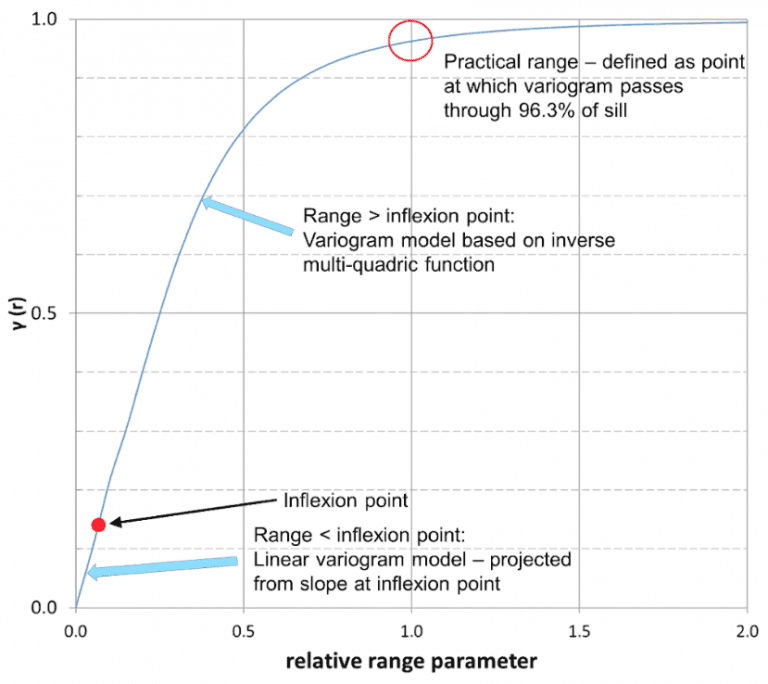
This figure shows the standard spheroidal variogram model for a range of 1. To develop a closed form expression for the spheroidals we will start with the generalised inverse multiquadric function and transform it to match these characteristics.
2. Constructing the Spheroidal variogram model
Following the definition in Chiles & Delfiner (page 86), the generalised Cauchy covariance can be written as:
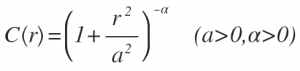
In this expression, r represents distance along the x axis, a represents a ‘range’ parameter and 𝒂 is the order to which the expression is raised. Note that the expression is here represented by C(r) reflecting that this is a covariance function.
2.1 Defining the family of multiquadric functions
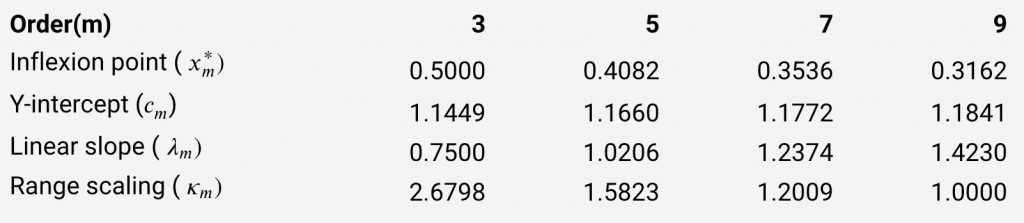
For analysis it is useful to consider the order of the covariance given by m = 2𝛼. In many applications, the values of m are restricted to odd integers, although the method can also be applied to general values of m. In Leapfrog we have chosen to only allow m = 3, 5, 7 or 9 and the derivation below will give the details for only those values.
To simplify the following derivation, we will let x = r/a. This allows us to re-write the right-hand side of the function in terms of the order of the function, and to express a simplification of the generalised form: the standardised inverse multiquadric function M of order m
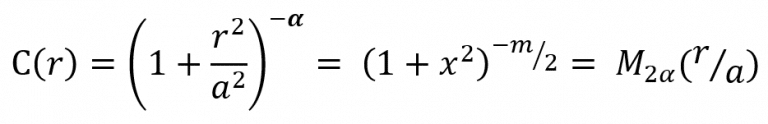
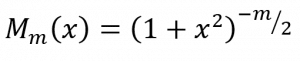
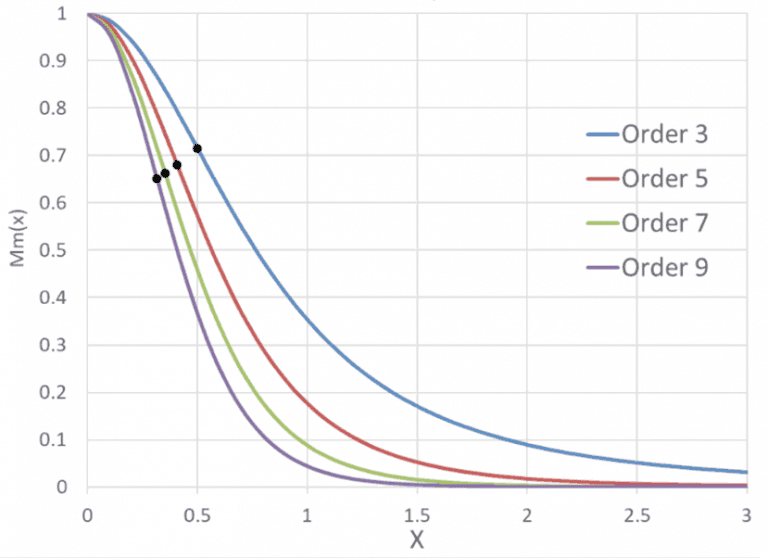
Graphs of the inverse multiquadric function of orders 3,5,7&9 are shown below in Figure 2. From these, one can see that the different orders of multi-quadric curve approach the asymptote of 0 at vastly different rates.
To convert the generalised inverse multiquadric covariance to a spheroidal variogram four steps are taken:
- Determine the inflexion point and add the correct linear section between it and the y-axis.
- Rescale the values of the function so that the y-intercept is again 1.
- Determine the correct scaling for the function argument so a practical range can be defined.
- Flip the function so it is in variogram form.
To begin with we’ll look at the first two stages and create a single piecewise function.
2.2 Creating the base covariance functions
The multiquadric has a unique inflexion point where the second derivative vanishes, that point is when:
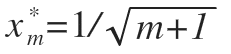
The value and gradient at this point can be used to project a straight line back to the y-axis, and to find the y-intercept at that point. That value is:
The inverse of this value is then used to scale the base function such that the rescaled function has a Y axis intercept of 1.
Using these constants, the base form of the covariance can be specified as a piecewise function ( Sm (x) ) that combines the linear section up to the inflexion point, and the scaled inverse multiquadric function after that.
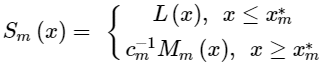
The linear section can be written as:
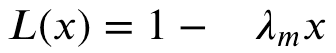
The value of the slope 𝜆m determined by the continuity of the function as:
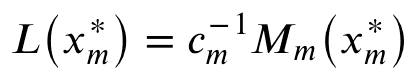
As it is a tangent, the gradients of the two parts are identical at that point as well. Following through the calculations:
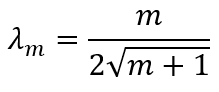
This base form of the covariance was used to prove the positive definite character of the family of spheroidal functions. A proof was given by Prof R.K. Beatson, University of Canterbury and can be provided on request.
2.3 Determining the variogram function
To convert the base covariance into a variogram function, the functions need to be flipped and an appropriate way of specifying a practical range needs to be developed. To do this we’ll borrow a concept from the another variogram function with an asymptotic sill – the exponential – and use a scaling of a range parameter to determine the correct argument for the spheroidal variogram.
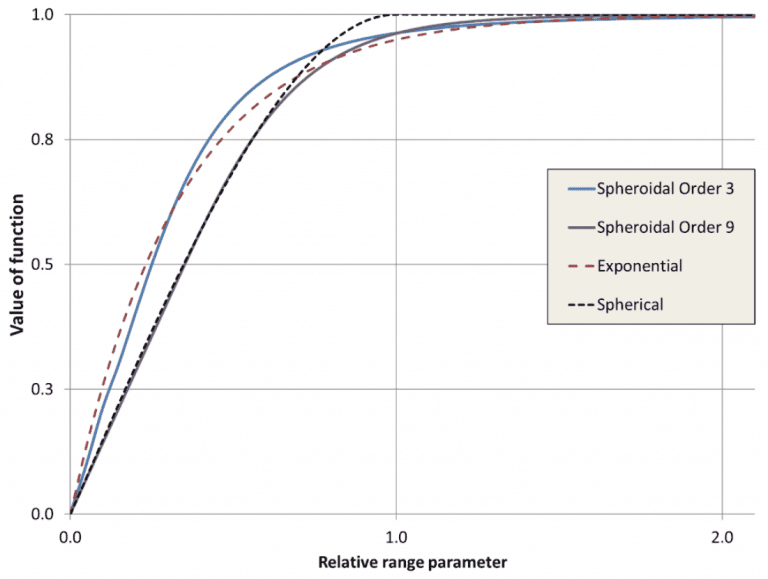
There is no universally accepted way of defining the range of a function that asymptotes to a sill. This difficulty is not faced for the common spherical variogram model as that reaches a sill at a defined range – it is intuitive that the range of the spherical variogram is the distance beyond which points are no longer spatially correlated.
For the exponential variogram which has form 𝛾exp = 1 − exp ( − r/a ), the practical range is typically taken as R ≈ 3a as the value there is ~95% of the sill. Reversing this relationship, one defines 𝛾exp,R = 1− exp ( − 𝜅 r/ R) , with the coefficient 𝜅 = 3, determining how to scale the relative value r/R.
For the spheroidals, we seek to do the same. If we define the spheroidal variograms as
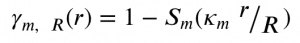
Then it remains to determine values of the coefficients 𝜅m so that the resulting variograms have a consistently defined and appropriate behaviour at the practical range r= R.
The choice of 3 for the exponential variogram was motivated by simplicity, and with that in mind, it can be observed that for order 9, the value of the base covariance is about 0.037 at x = 1. This means if we use 𝜅9=1, then the spheroidal variogram of order 9 will have a value at the practical range that is about 96.3% of the sill.
For consistency, this value will also be used for calculating the other coefficients and we will solve 𝛾m,R (R)= 𝛾9,R(R) for 𝜅m This leads to the equation Sm(𝜅m) = S9(1). Writing the right-hand side as a constant
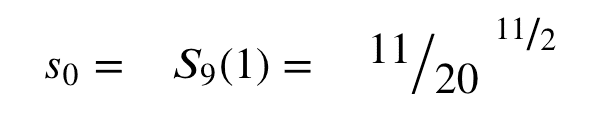
The expression can be solved to find 𝜅m:
A piecewise expression for the full spheroidal variogram can then be written out:
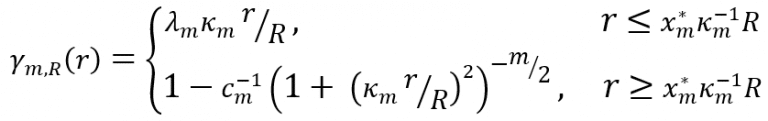
Comparison
The table of constants for the four orders provided in Leapfrog is as follows (values to 4dp):
The resulting variogram models for a range of 1 can be compared with the standard spherical and exponential variograms in the following figure.